Algoritmos Gulosos - Introdução

paradigmas • 5 de Jun de 2020

Um algoritmo guloso constrói a solução sempre tomando uma decisão que parece a melhor localmente, esperando que esta leve a solução ótima globalmente. Portanto, eles são incisivos em suas decisões, não voltam atrás em uma decisão tomada, e sim constroem a solução diretamente. Por esta razão, em alguns casos, soluções gulosas funcionam e são curtas. Mas problemas que envolvem este paradigma devem conter essas duas características(segundo o CP3):

Possui subestruturas ótimas: A solução ideal para o problema contém soluções ótimas para os subproblemas.
Possui a característica gulosa: Se fizermos uma escolha que pareça a melhor localmente e continuarmos a resolver o problema, chegaremos à solução ideal. E nunca teremos que reconsiderar uma decisão anterior.

Depois de um pouco de formalidade, esse é um dos paradigmas que se explica melhor dando exemplos.

Exemplos:

E nada melhor para começar a exemplificar que.........

Notas e moedas.

Captura-de-tela-de-2020-06-01-17-14-38

Não, não é aqui que vou te ensinar como passar esse problema. Mas uma solução possível para esse problema é greedy, e no entanto, para efeito de exemplo, não vou usar o notas e moedas, e sim o problema cédulas que tem o exato mesmo funcionamento e a solução é análoga, só que não tem as moedas rsrs.

No problema o objetivo é chegar a um valor N usando o menor número de cédulas. As cédulas consideradas no problema são: [1, 2, 5, 10, 20, 50, 100].

Então para um valor, por exemplo, de 576 a solução ótima seria: 5 * 100 + 1 * 50 + 1 * 20 + 1 * 5 + 1 * 1.

Observando este caso, dá pra perceber que uma solução gulosa simples para o problema é: sempre escolher a maior cédula possível e tirar do valor total. Mas, beleza, esse algoritmo funciona no primeiro caso de teste: Primeiro tiramos 500 em notas de 100, ficando com 76; tiramos então 50 com uma nota de 50, ficando com 26; retira-se 20 com uma nota de 20, sobra 6; aqui a melhor escolha é tirar uma nota de 5, ficando com um, pôr fim usamos uma nota de 1.


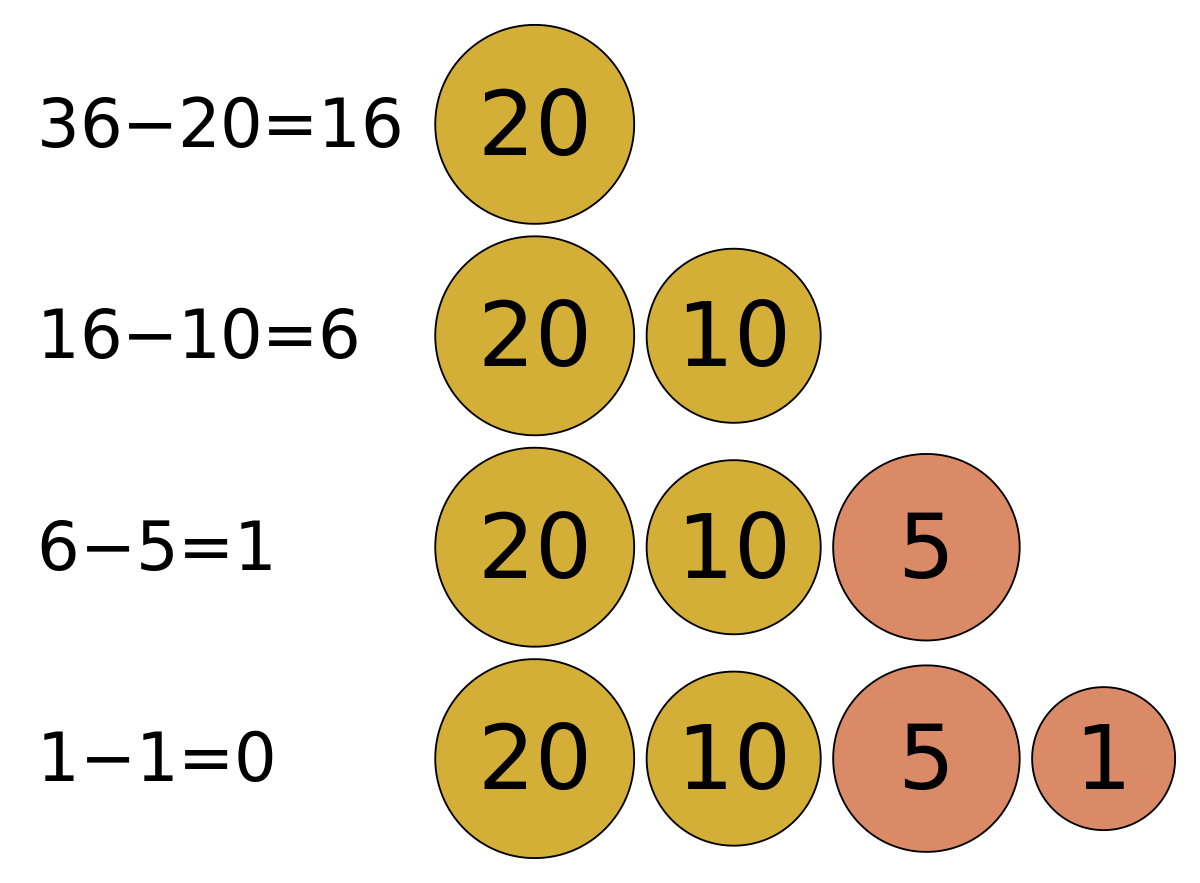fonte: https://en.wikipedia.org/wiki/Greedy_algorithm

A complexidade geral é O(n), ou seja passa para limites N = ~1000000.

O que fizemos aqui foi fazer sempre a melhor escolha local, sem voltar atrás nas decisões. E será que este funcionará em todos os casos?

Acontece que para esse determinado set de moedas sim, a solução greedy sempre vai produzir o menor número de notas. E a explicação de porque funciona vem a seguir:

Primeiro, cada moeda 1, 5, 10 e 50 vão aparecer no máximo uma vez na solução, pois se a solução aceita duas dessas moedas nós podemos às substituir por uma e produzir uma resposta melhor. Por exemplo: 5+5, podemos substituir por uma nota de 10. Do mesmo jeito, as moedas 2 e 20, vão aparecer no máximo duas vezes na solução ótima, pois 2+2+2 podemos substituir por 5+1 e 20+20+20 por 50+10. Além disso, a solução ótima não vai conter 2+2+1 e 20+20+10, que são substituíveis por 5 e 50.

A partir dessas informações, percebe-se que não tem como escrever um valor x que seja igual a uma nota ou maior que, de modo ótimo usando moedas menores que x.

Este exemplo também demonstra que é difícil provar que uma solução gulosa funciona, até mesmo se a o algoritmo é simples. E um bom jeito de mostrar quando funciona é também mostrando quando não funciona:

Exemplo que não funciona

Uma informação que pode parecer genérica mas não é, é o set de moedas. Pois, para outros sets de moedas esta solução pode facilmente ser descartada. Por exemplo: [1, 3, 4] tendo que alcançar o valor 6, o nosso algoritmo ia chegar a: 4+1+1 usando 3 moedas, porém a resposta ótima seria 3+3 usando 2 moedas.

Um bom jeito de visualizar algoritmos gulosos é vendo eles funcionando em grafos:


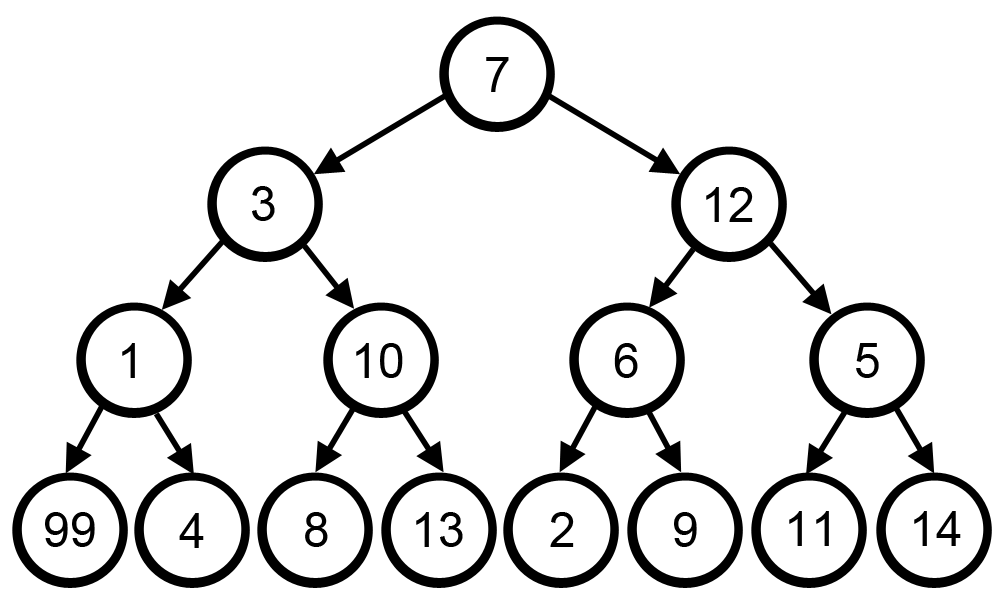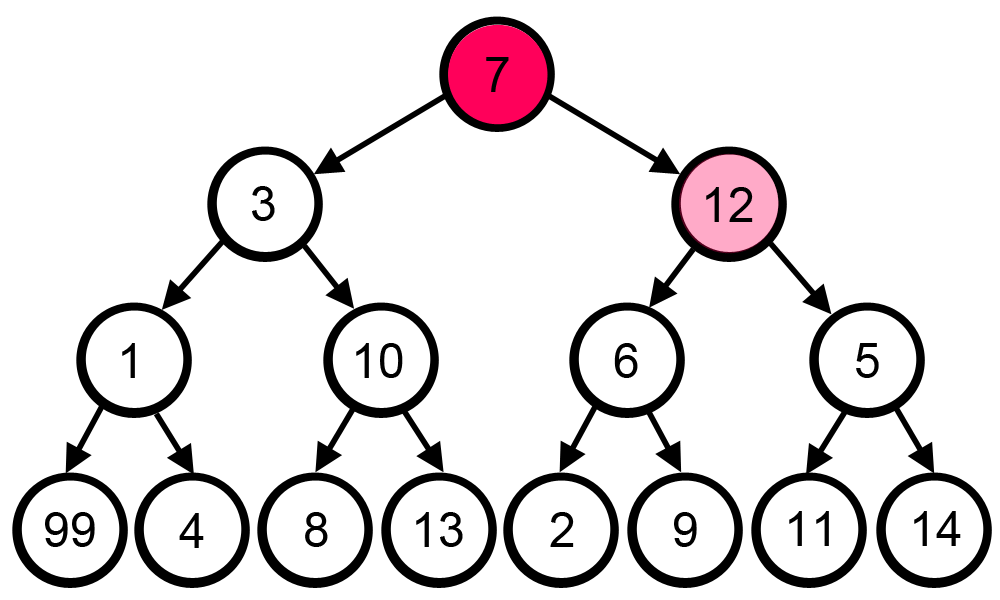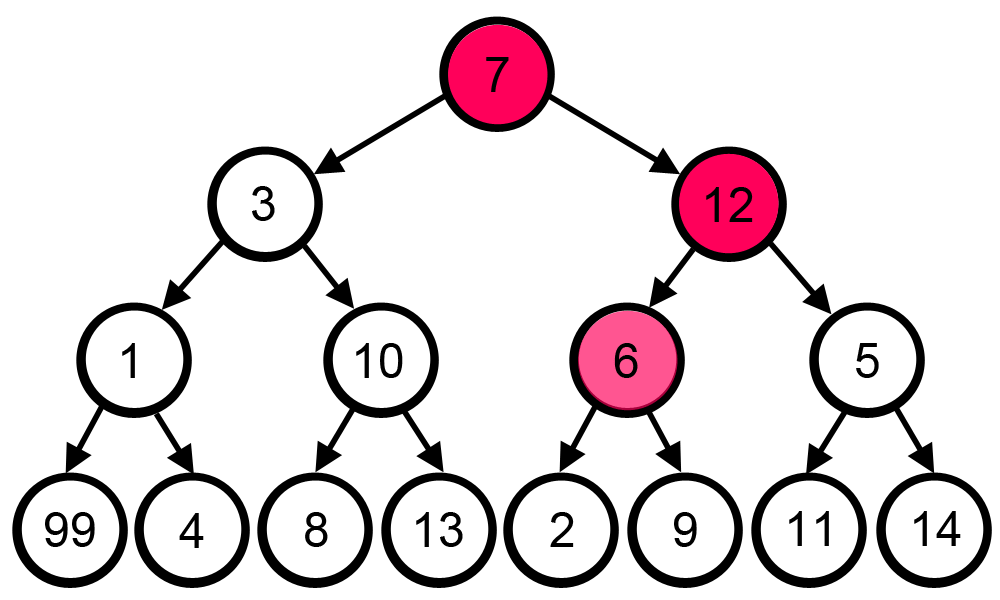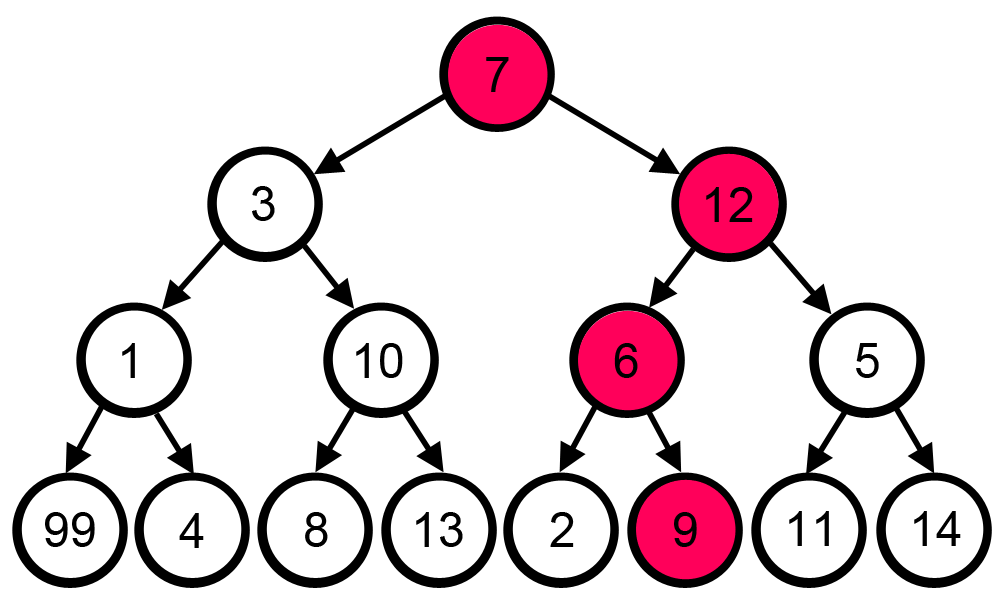fonte: https://es.wikipedia.org/wiki/Algoritmo_voraz

Com o objetivo de maximizar a soma no caminho escolhido, a estratégia greedy foi usada: em uma bifurcação, ir para o nó de valor maior. é visível que esta estratégia não chega ao resultado ótimo.

Talvez esse seja o motivo de usarmos esse sistema monetário.

Problemas com esse tipo de set tem sua solução ótima resolvida por outro paradigma: programação dinâmica.


fonte: O autor

Conclusão

Concluindo. Algoritmos gulosos são poderosos, pois são geralmente a primeira solução a ser pensada, são de rápida e simples implementação e geralmente são rápidos. Tem como contraponto eles serem difíceis de provar - sempre bom tentar fazer um caso de teste para quebrar -, e as vezes o O(n) não passa.

Esse post foi uma breve introdução ao tema, pretendo produzir mais alguns indo até os possíveis tópicos mais avançados.